오메가
쉽게 이야기하면 각이 지니는 속도(=각속도)로 말할 수 있고, 이것은 모터의 회전수 rpm이라 보시면 됩니다. 마찬가지로 각속도 w(오메가)도 초당 얼마나 회전하는 가를 나타냅니다. w=2*pi*f 에서 2*pi는 원주율로 지름에 비해서 원의 둘레가 얼마나 커지는가를 나태나는 비례상수인건 아실거구요. f는 주파수로 결국 주파수가 높으면 각주파수는 높아지는 것이겠죠.
람다
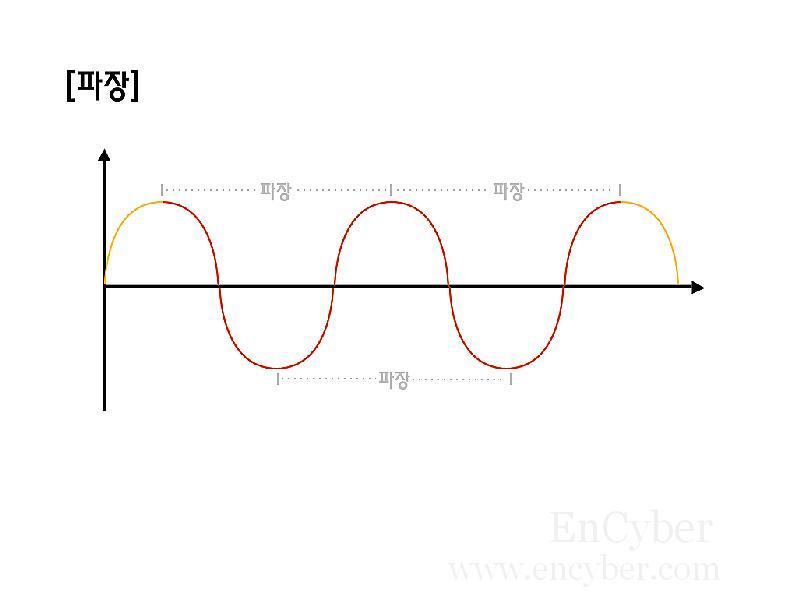
파장은 마루, 골과 같이 파동의 공간적 특징을 기술하는 몇 가지 중요한 용어 중 하나이다. 시간의 흐름을 멈춰 한 순간 정지된 물결 파를 물결을 가로지른 단면을 통해 관찰해 보자. 그림처럼 하나의 일정한 모양이 주기적으로 반복해서 나타남을 쉽게 알 수 있다. 파장은 이렇게 반복되는 모양이 어느 정도의 길이마다 반복되어 다시 나타나는가를 나타내는 양으로써 한 마루에서 이웃한 마루까지의 거리 또는 한 골에서 이웃한 골까지의 거리를 측정함으로써 구할 수 있다.
진동수
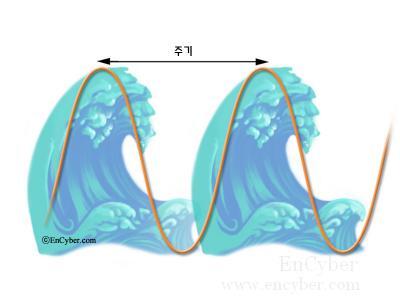
주기와 진동수의 관계
진동 현상에서 진동수는 단위 시간 동안 위와 같은 왕복 운동이 일어나는 횟수로써 정의되어 있다. 주기는 한 번의 왕복운동이 일어날 때 걸리는 시간이므로 단위 시간에다 진동수를 나눠 주면 주기를 얻을 수 있음을 쉽게 유추할 수 있을 것이다. 위 예제를 다시 검토해 보아도 그러한 방법으로 주기가 계산되었음을 알 수가 있다.
이 관계를 수식으로 나타내면 진동수를 f, 주기를 T라고 할 때 T=1/f의 수학적 관계가 성립한다. 이 식에 의해서 주기를 알면 진동수를 구할 수 있고 진동수를 알면 역으로 주기를 계산할 수 있게 된다.
ㄴㅇ
A라는 지점에 파동의 마루가 있고, L이라는 지점에 두번째 파동의 마루가 있다고 합시다. 그러면 파동의 주기는 마루에서 마루까지 혹은 골에서 골까지 한파장 진행하는데 걸린 시간을 얘기합니다. 그래서 파동의 주기는 0.5초가 되는 거구요, 파동의 파장은 마루에서 마루까지 혹은 골에서 골까지의 거리를 나타내는 겁니다. 문제에서 그 거리가 10m이므로 파장이 10m가 되는 것이죠~ 그럼 파동의 속도는 어떻게 구하냐하면요~ 속도라는 것은 거리를 시간으로 나누면 되잖아요 즉, v = s/t 파동에서 거리는 파장이 되고요, 시간은 주기가 되거든요~ 그래서 파동의 속도 v = 10/0.5 하면 됩니다. 그래서 20m/s가 답이됩니다.
그리고 참고로 주기와 역수의 관계에 있는 주파수(진동수)라는 것이 있거든요, 이것은 1초에 파동이 몇번 생기느냐 하는 것이죠. 주파수는 기호로 f라고 나타내고 단위는 Hz를 사용합니다. f = 1/T 이죠~
